 |
The
Sundial Primer created by Carl Sabanski |
 |
 |
The
Sundial Primer created by Carl Sabanski |
 |
|
DeltaCad Sundial Macros - Valentin Hristov - Foster-Lambert Sundial A typical analemmatic sundial consists of hour points positioned on an ellipse, a date scale and a moveable gnomon. The gnomon for a horizontal analemmatic sundial is vertical. If the gnomon's angle is suitably adjusted it is possible to end up with a circular ring of equiangular hour points. This is a Foster-Lambert sundial. The following macro by Valentin Hristov will draw not only a typical horizontal sundial but such a sundial in any orientation. Foster-Lambert Sundial - fl The Foster-Lambert sundial is generated after the user enters the "Latitude", "Longitude", "Central meridian", "Declination of the plane" and "Inclination of the plane" of the sundial's location as shown in Figure 1. A "Place" descriptor can also be included. The Equation of Time is accounted for by a graph. Longitude correction can be removed by entering the same value for "Longitude" and "Central meridian".
Figure 1 - Foster-Lambert Sundial Macro The sundial drawn with this macro is shown in Figure 2. This example is a horizontal sundial. Note the hour points are arranged on the circumference of a circle and are spaced at equal angles. All 24 hours are included. The sundial will not normally show all the hours and the ones that should remain depends upon the latitude. The hour points are adjusted for longitude and an EoT graph is included. The gnomon is drawn at an angle relative to the vertical line of the date scale. This angle is given by the parameter "g" in the table to the right of the sundial and for this horizontal sundial is equal to (90 + Latitude) / 2.
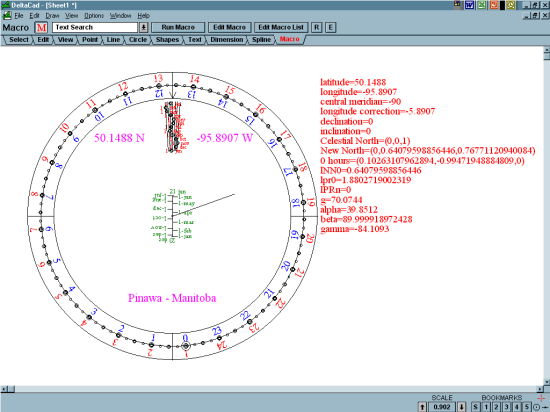
Figure 2 - Foster-Lambert Sundial It is important to remember that the gnomon must be placed on the date scale at the proper angle as shown by the projection on the date line. The gnomon's angle is indicated with respect to centre the date line. Both the gnomon and the text on the right should be removed before the final printing. Use the "Select" tab and the "Er" (Erase) button in DeltaCad. The hour ring should be made movable in order to adjust for the Equation of Time. Rotate the ring so the arrow at the top of the ring points to the date on the stationary central circular area.
|